标题

广义非线性三维Hoek‒Brown破坏准则

A generalized nonlinear three-dimensional Hoek‒Brown failure criterion

期刊

Journal of Rock Mechanics and Geotechnical Engineering

链接

https://doi.org/10.1016/j.jrmge.2023.10.022

作者

王佳信，吴顺川*，程海勇，孙俊龙，王晓龙，沈亚玺

广义Hoek‒Brown准则可反映岩石和岩体固有的非线性破坏特点，40余年来，关于Hoek‒Brown准则的各类表达式超过30种，其中，不乏具有新意的研究，部分学者在理论上有所突破，但大部分修正的Hoek‒Brown准则仍停留在完整岩石强度的研究上。针对岩体强度的研究仍普遍采用岩体分级系统对岩体质量进行评价，基于经验方法获取岩体参数，进而确定岩体强度，未来很长时间内，经验法确定工程岩体强度仍为主流方法。因此，提出一种广义非线性三维Hoek‒Brown破坏准则，对构建工程岩体强度具有重要理论意义和工程价值。

昆明理工大学吴顺川教授牵头的“深地资源开发与灾害防控创新团队”在Journal of Rock Mechanics and Geotechnical Engineering期刊上发表了题为“A generalized nonlinear three-dimensional Hoek‒Brown failure criterion”的文章，该文章提出了一种广义非线性三维Hoek‒Brown破坏准则，并采用大尺度原位岩体试验结果作为验证数据，进而可为复杂应力路径下原位工程岩体强度准则构建奠定前期基础理论。

论文介绍

为研究复杂应力状态下岩石的强度，本文提出了一种广义非线性三维Hoek‒Brown破坏准则(NGHB准则)，该准则与广义Hoek‒Brown准则共享同一套参数体系，完全继承了广义Hoek‒Brown准则中参数取值的优势。NGHB准则中引入两个新的材料参数β和n，其物理意义明确，即分别主要控制三轴拉伸和三轴压缩条件下NGHB准则的偏平面形状。NGHB准则解决了广义Hoek‒Brown准则中破坏包络面未满足光滑性以及未考虑中间主应力等问题，该准则可退化为现有2种修正三维Hoek‒Brown准则、三轴压缩条件下的Priest准则以及三轴压缩和拉伸条件下的HB准则。

采用不同参数、6种岩石及2种原位岩体的真三轴试验数据对NGHB准则进行验证，并选取3种现有三维Hoek‒Brown准则进行性能对比研究。结果表明，NGHB准则比其他准则具有较好的预测性能，6种岩石及2种原位岩体的强度预测误差分别在2.0724%‒3.5091%和1.0144%‒3.2321%范围内。

此外，本文开发了名为NGHB准则的MATLAB应用程序，该程序可具有可视化功能，可根据岩石强度的预测误差值直观地判断各准则的性能，可为复杂应力路径下原位工程岩体强度的构建奠定前期基础理论。

文章亮点：

(1) 提出了一种广义非线性三维Hoek‒Brown破坏准则(NGHB准则)；

(2) 完善了三维Hoek‒Brown准则的理论框架，所提NGHB准则可退化为多个现有的三维Hoek‒Brown准则以及三轴压缩和拉伸条件的HB准则；

(3) 开发了MATLAB应用程序，基于该程序可根据岩石强度的预测误差值直观判断各准则性能。

图文解析

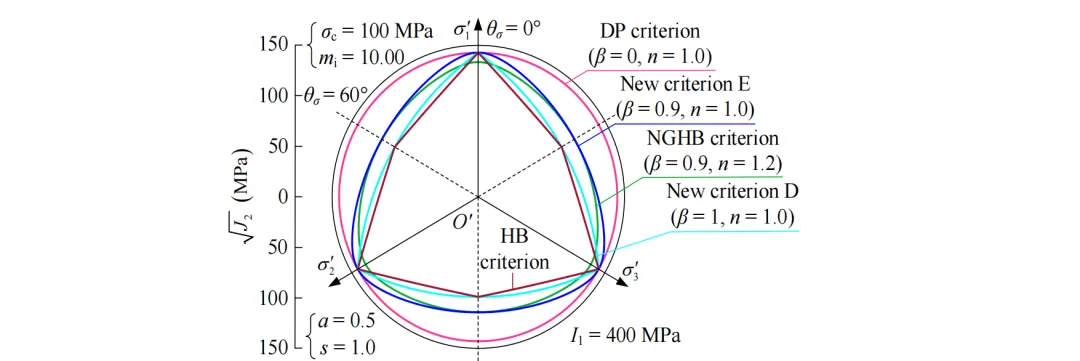
图1 偏平面上参数β和n对NGHB准则破坏包络线的影响

当参数β∈[0, 1]和n = 1时，NGHB准则退化为新准则E(Jiang, 2017)；当参数β = 1和n = 1时，NGHB准则退化为新准则D (Jiang and Zhao, 2015)；当n = 1和β = 0时，NGHB 准则的破坏包络线为Drucker–Prager准则的一个圆；当β = 1、n = 1和θσ = 0°时，NGHB准则退化为三轴压缩条件下的Priest准则(Priest, 2005)。此外，NGHB准则还可退化为三轴压缩和拉伸条件下的HB准则。

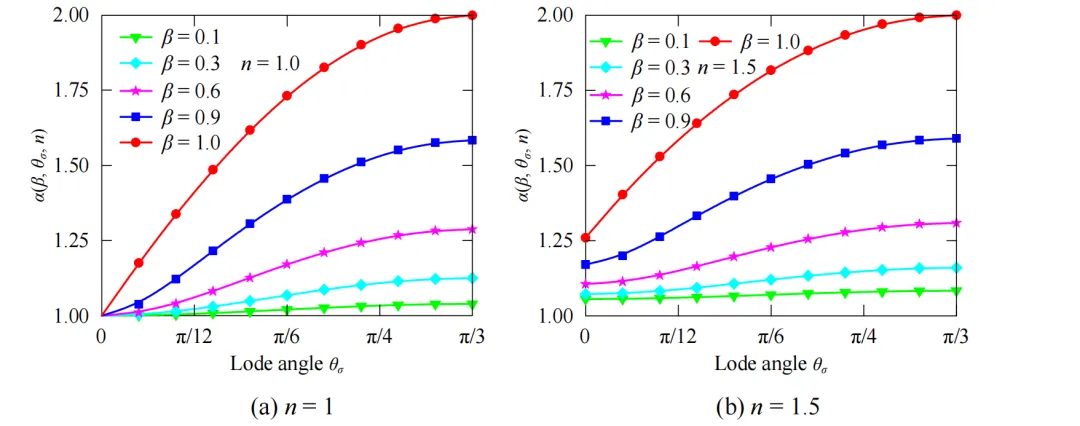
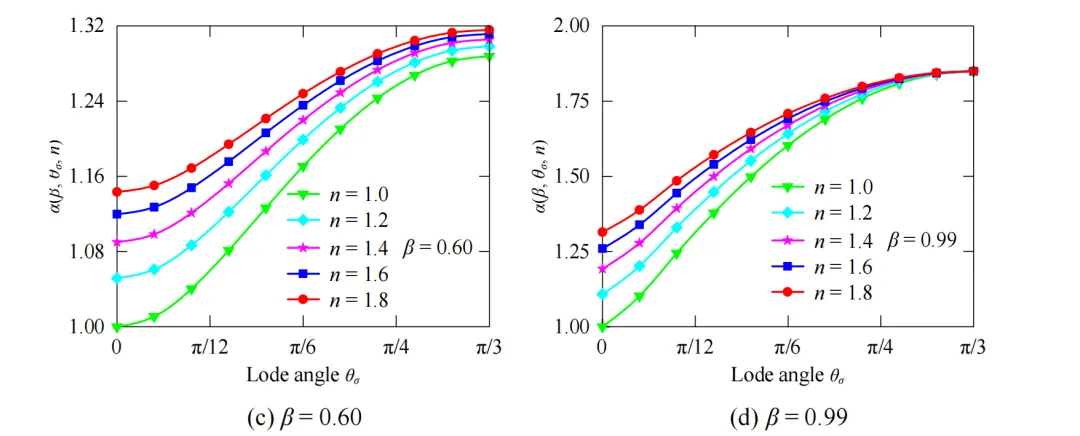
图2 不同参数β和n下函数α(β, θσ, n)的变化规律

对比图2(a)‒(b)研究发现，NGHB准则中参数n对三轴压缩状态下的偏平面形状起主导作用，对三轴拉伸状态下的偏平面形状有一定的影响。对比图2(c)‒(d)研究发现，NGHB准则中参数β对三轴拉伸状态下的偏平面形状起主导作用，对三轴压缩状态下的偏平面形状有一定的影响。

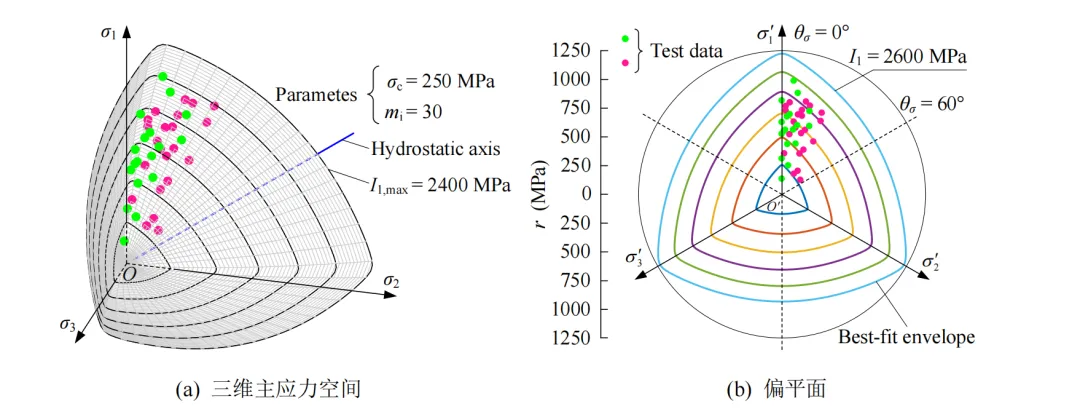
图3 NGHB准则(β = 0.99, n = 1.3)下KTB角闪岩的二维、三维最佳拟合结果

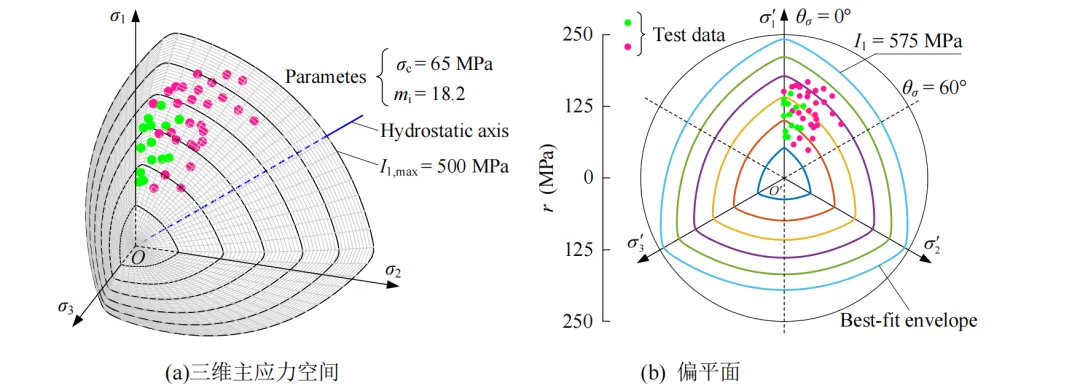
图4 NGHB准则(β = 0.99, n = 1.5)下Shirahama砂岩强度的二维、三维最佳拟合结果

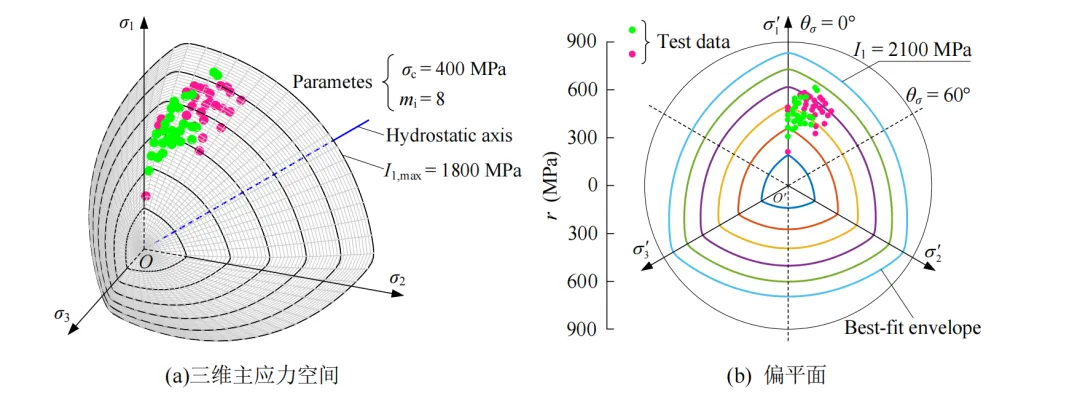
图5 NGHB准则(β = 0.99, n = 1.6)下Dunham白云岩二维、三维最佳拟合结果

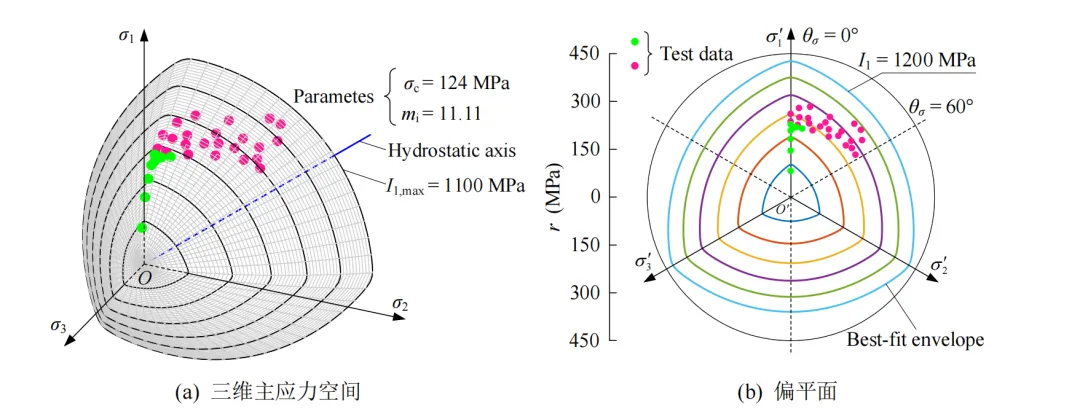
图6 NGHB准则(β = 0.99, n = 1.5)下Mizuho粗面岩二维、三维最佳拟合结果

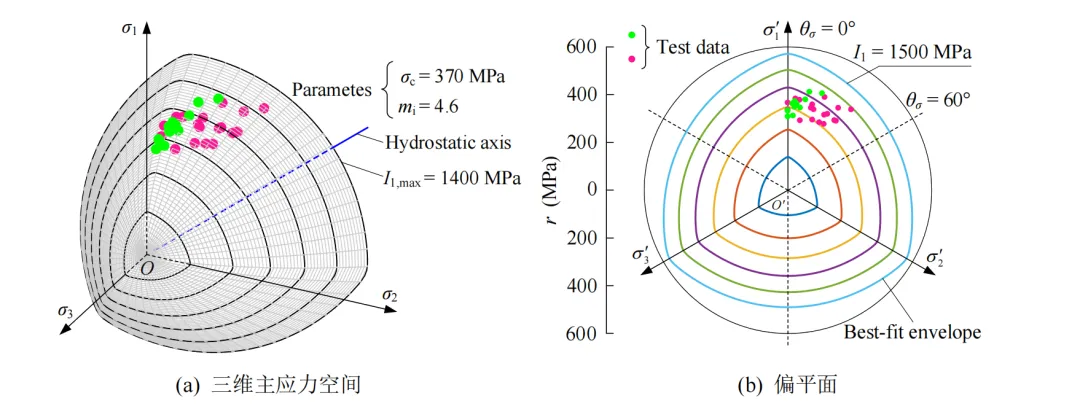
图7 NGHB准则(β = 0.99, n = 1.6)下Solnhofen 石灰岩二维、三维最佳拟合结果

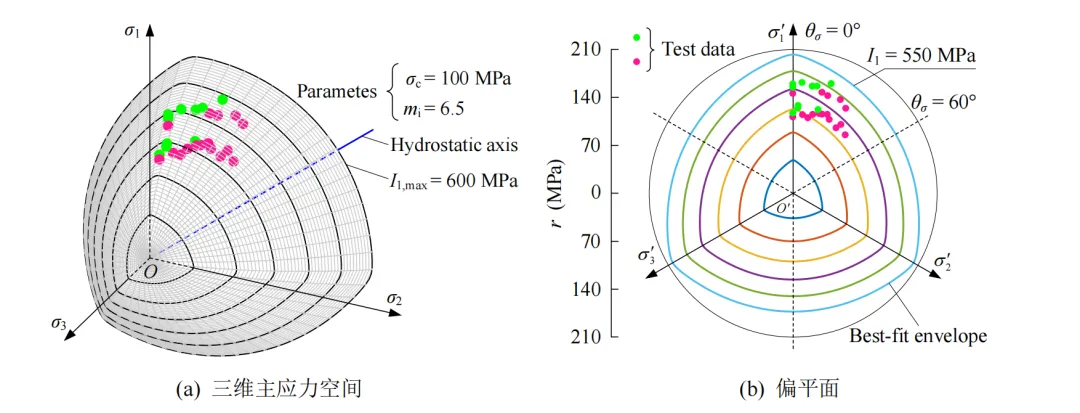
图8 NGHB准则(β = 0.99, n = 1.6)下Yuubari板岩二维、三维最佳拟合结果

图3‒8为三维主应力空间、偏平面上最佳拟合结果与真三轴试验数据的对比结果，可看出6种岩石的真三轴试验数据中分别有18(总共40)、14(总共42)、27(总共53)、8(总共31)、11(总共30)和10(总共26)组试验数据(绿色圆点)分布在最佳拟合包络面上方，6种岩石的真三轴试验数据较均匀地分布在破坏包络面上下附近，且三维破坏包络面表现出光滑、外凸的非线性特征。

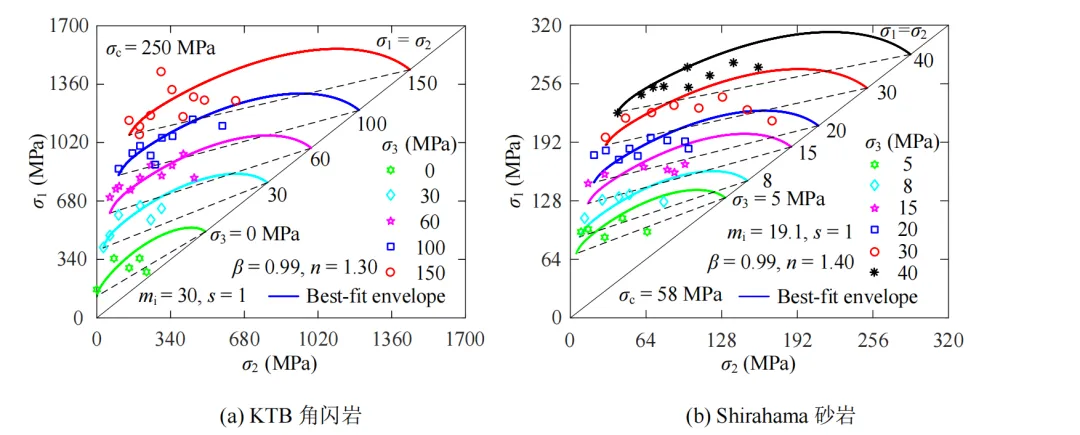
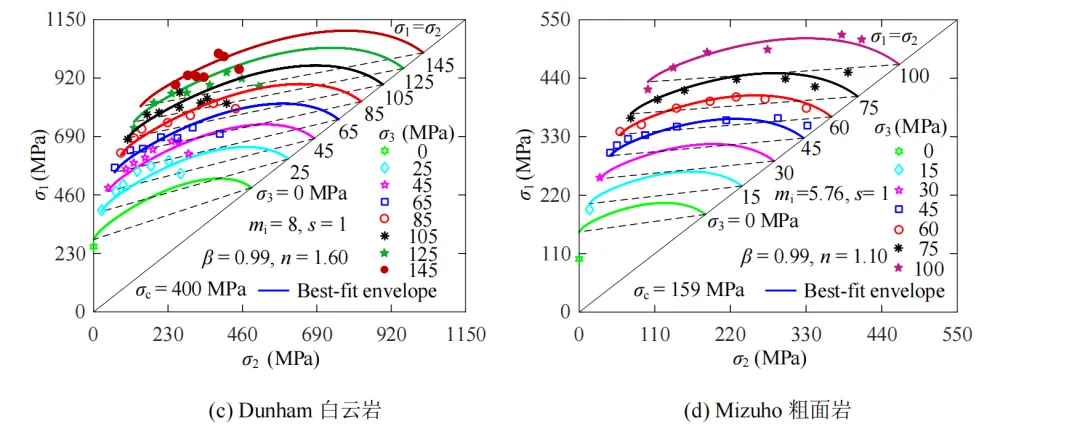
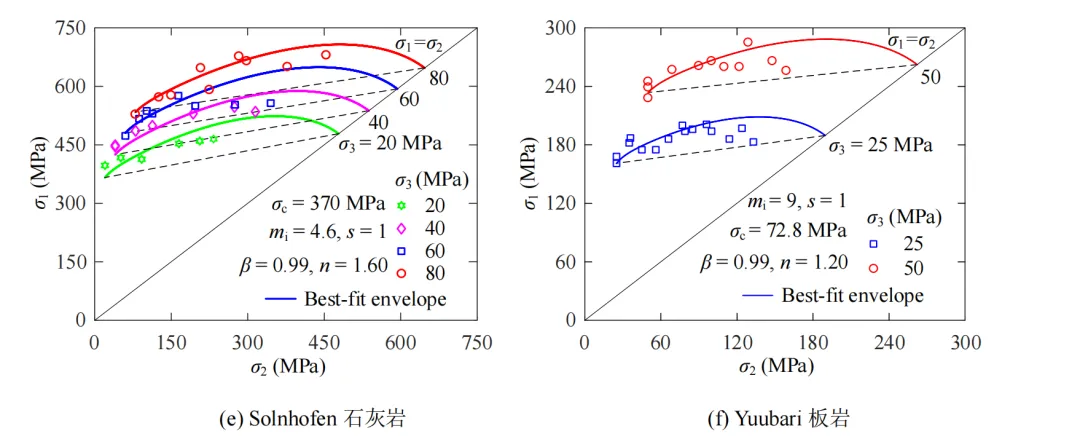
图9 σ1‒σ2平面上NGHB准则对6种岩石强度的拟合结果

由图9可看出，σ1‒σ2平面上NGHB准则能较好地描述6种岩石强度随中间主应力σ2的增大呈“先增后减”的趋势，且试验数据较均为分布在破坏包络线上下附近。

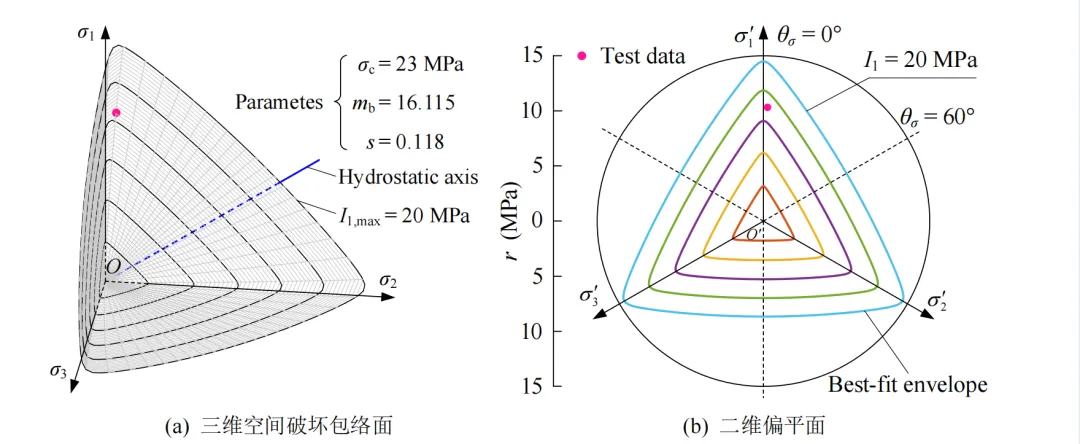
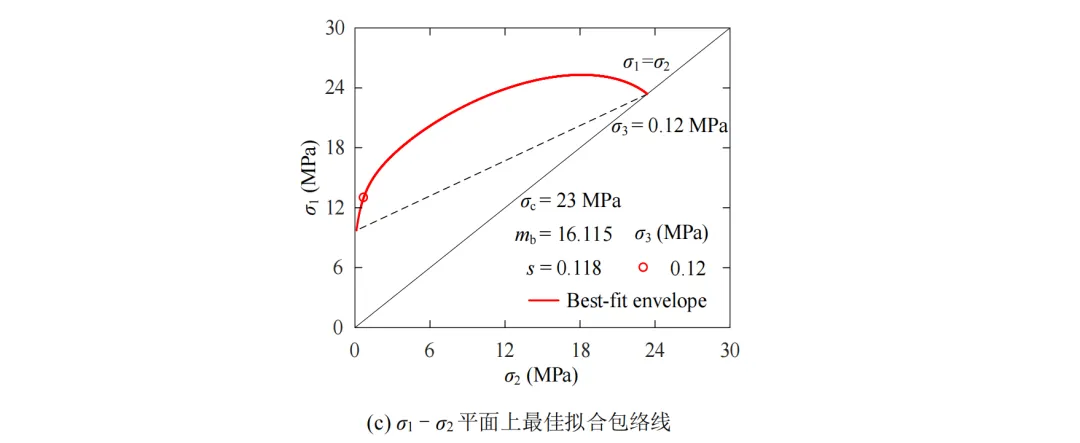
图10 NGHB 准则下日本Kurobe IV拱坝地基花岗岩岩体强度的最佳拟合结果(n =1.02）

由图10可看出，NGHB准则的三维破坏包络面表现出非线性特征，低静水压力下该准则的偏平面形状呈光滑、外凸的曲边三角形，σ1‒σ2平面上该准则能较好地描述花岗岩岩体强度随中间主应力σ2的增大呈“先增后减”的趋势。

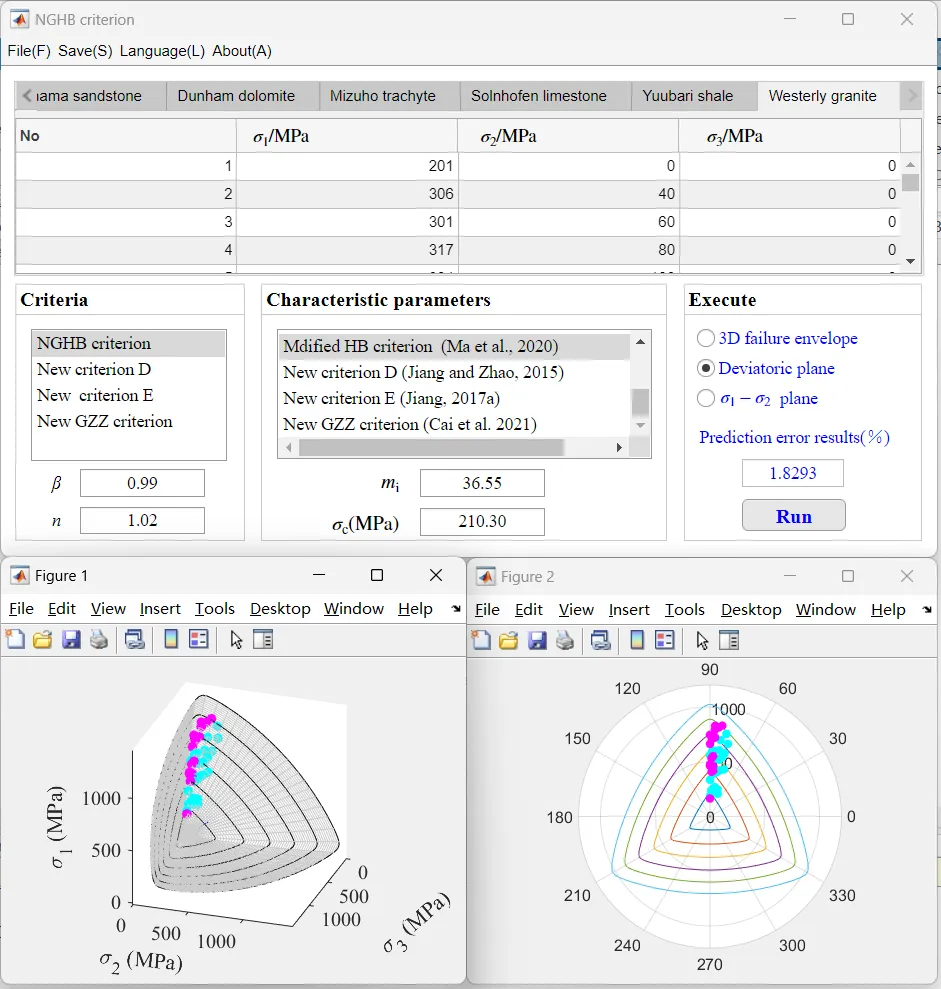
图11. MATLAB app操作界面

手动输入材料参数β和n，选择相应的图形按钮，点击Run即可浏览图形和查看岩石强度的预测误差值。MATLAB app下载网址如下：

https://github.com/KUSTWang/NGHB_criterion.git.

 

 

团队简介

 

 

昆明理工大学“深地资源开发与灾害防控科技创新团队”，在国家高层次人才吴顺川教授的带领下长期从事科研与教学工作，现有68名科研⼈员(包括国家⾼层次⼈才1名、云南省⾼层次⼈才6名、教授4名、副教授4名、⾼级⼯程师1名、讲师4名、博⼠研究⽣11名、硕⼠研究⽣45名)。研究团队凝聚岩⽯⼒学、边坡⼯程、地下⼯程、膏体充填及测绘⼯程等科技⼈才，围绕矿⼭、交通等⾏业岩体⼒学⾏为、岩体稳定性、⼯程灾害安全预警等前沿领域，始终坚持“产、学、研”紧密结合的理念，共承担30余项纵向科研课题，提出的大断面软弱岩层隧洞新型支护方案在滇中引水工程楚雄段进行了成功试验，成功探索了我国超大断面软岩地下工程新型施工工法，开创了我国超大断面软岩地下工程施工工法的突破；发表高水平论⽂400余篇(其中SCI/EI论文300余篇)，授权专利80余项、授权软件著作权10余项，1人入选Elsevier 2023“中国高被引学者”，实现了云南省采矿工程学科高被引学者的首次突破；获得国家科技进步奖2项，省部级奖励20余项，承办国内外学术会议13次，参加国内外学术会议50余次；团队教师一直致力于高等教学教育改革工作，近五年承担6项国家与省部级教改项目，先后荣获省部级教学成果奖4项，主编出版教材/论著10余部，其中《岩石力学》新形态教材被全国100余所高校选用，受到国内外15名院士寄语好评及一线教师和专家学者普遍好评，其中国家最高科学技术奖获得者钱七虎院士评价其为“一本多年教学经验总结、集体智慧结晶的好教材”。依托团队成立的深地资源开发与灾害防控科技创新党支部，始终坚持以习近平新时代中国特色社会主义思想为指导，全面贯彻党的二十大精神，先后被教育部遴选为第四批全国党建工作“样板支部”培育创建单位、被中共云南省委教育工委选为第五批高校一流党建示范“双带头人”工作室、被中共昆明理工大学委员会选树为一流党建示范党支部以及评为“先进基层党组织”。

 

 

 

近年团队在岩石强度理论方面发表的文章：

[1] S.C. Wu, S.H. Zhang, C. Guo, and L.F. Xiong, A generalized nonlinear failure criterion for frictional materials, Acta Geotech., 12(2017), No. 6, p. 1353.

[2] S.C. Wu, S.H. Zhang, and G. Zhang, Three-dimensional strength estimation of intact rocks using a modified Hoek–Brown criterion based on a new deviatoric function, Int. J. Rock Mech. Min. Sci., 107(2018), p. 181.

[3] S.H. Zhang, S.C. Wu, and G. Zhang, Strength and deformability of a low-porosity sandstone under true triaxial compression conditions, Int. J. Rock Mech. Min. Sci., 127(2020), art. No. 104204.

[4]Wu S, Wang J, Zhang S, et al. Retrospective and prospective review of the generalized nonlinear strength theory for geomaterials[J].Int. J. Miner. Metall. Mater., 2024, 31(8): 1767-1787.

[5] J.X. Wang, S.C. Wu, X.K. Chang, H.Y. Cheng, Z.H. Zhou, and Z.J. Ren, A novel three-dimensional nonlinear unified failure criterion for rock materials, Acta Geotech., (2023), p. 1.

[6] P. Guo, S.H. Zhang, and S.C. Wu. Strength characteristics and double‒yield Elastoplastic Constitutive Model of Granite. Geotech. Geol. Eng. 2024: 1-17. DOI:10.1007/s10706-024-02864-8.

[7] 吴顺川，张敏，张诗淮，等.修正Hoek‒Brown准则的等效Mohr‒Coulomb强度参数确定方法研究[J].岩土力学，2019，40(11)：4165‒4177.

[8]吴顺川，姜日华，张诗淮，等.修正Hoek‒Brown强度准则在钻孔稳定性分析中的应用[J].岩土力学，2018，39(S2)：1‒13.

[9] 张诗淮，吴顺川，吴昊燕.岩石真三轴强度与Mohr‒Coulomb准则形状函数修正方法研究[J].岩石力学与工程学报，2016，35(S1)：2608‒2619.

引用本文

Wang, J.X., Wu, S.C., Cheng, H.Y., Sun, J.L., Wang, X.L., Shen, Y.X., 2024. A generalized nonlinear three-dimensional Hoek‒Brown failure criterion. J. Rock Mech. Geotech. Eng. 2024, 16 (8), 3149‒3164. https://doi.org/10.1016/j.jrmge.2023.10.022.

END